4.85
24 reviews
Mastering Complex Calculus: From Derivatives to Residues
Complex Calculus: derivatives of complex variables, contour integration, Laurent series, Fourier series, and residues
- Description
- Curriculum
- FAQ
- Reviews
Complex Calculus is an essential course that provides students with a foundation in complex functions, derivatives of complex variables, contour integration, Laurent series, Fourier series, and residues. In this course, you will learn the key concepts of Complex Calculus, and the process of reasoning by using mathematics, rather than rote memorization of formulas and exercises. Here’s what you need to know about this course:
- Introduction to Complex Functions: The course begins by focusing on the concept of complex functions.
- Derivatives of Complex Variables: Next, the concept of derivative is extended to functions of a complex variable.
- Contour Integration: You will learn about contour integration, and the following theorems will be derived: Cauchy’s integral theorem and Cauchy’s integral formula.
- Laurent Series: The Laurent series will be mathematically derived. From Laurent, the Fourier and Taylor series are also derived.
- Residues: You will be introduced to residues and how to use them to do contour integration.
- Prerequisites: To take this course, you should have completed single variable Calculus, especially derivatives and integrals, and multivariable Calculus, especially line integrals and Stokes’ theorem.
- Original Material: This course is based on the instructor’s notes on Complex Calculus, and the presentation of the results is therefore original.
- Focusing on Understanding: The explanations are given by focusing on understanding and mathematically deriving the key concepts, rather than learning formulas and exercises by rote.
- Benefits: Some of the results presented in this course constitute the foundations of many branches of science, including Quantum Mechanics, Quantum Field Theory, and Engineering (in the Control theory of dynamical systems, for instance). By mastering the contents of this course, you will be able to tackle the most interesting mathematical and engineering problems.
- Who this course is for: This course is suitable for anyone interested in expanding their knowledge of mathematics, including students of mathematics, physics, engineering, and related fields, as well as professionals who wish to develop their understanding of Complex Calculus.
Integration in Complex Calculus
Laurent Series, Fourier Series, Taylor Series
Residues and Contour Integration
How residues aid in the interpretation of the Fourier Transform and its inverse
-
13Concept of ResidueVideo lesson
-
14Residue TheoremVideo lesson
-
15Calculation of residues and coefficients of the Laurent seriesVideo lesson
-
16Evaluation of a real integral using complex integration (exercise 1)Video lesson
-
17Contour integration to evaluate a real integral (exercise 2)Video lesson
-
18Contour integration to evaluate a real integral (exercise 3)Video lesson
-
19Another integral evaluated using the results of Complex Calculus (exercise 4)Video lesson
-
20Contour integration to evaluate a complex integral (exercise 5)Video lesson
-
21Another contour integration of a real integral - Exercise 6Video lesson
-
22Fresnel integral over the real line (formally derived with the residue theorem)Video lesson
-
23Hilbert transform and its geometric meaningVideo lesson
-
24Solution to the diffusion equation using complex calculus and Laplace transformVideo lesson
-
25Representation of the Dirac DeltaVideo lesson
-
26Abel-Plana formula in complex CalculusVideo lesson
-
27Convolution of sinc functions using complex calculusVideo lesson
How to use complex calculus to attribute meaning to divergent series
How long do I have access to the course materials?
You can view and review the lecture materials indefinitely, like an on-demand channel.
Can I take my courses with me wherever I go?
Definitely! If you have an internet connection, courses on Udemy are available on any device at any time. If you don't have an internet connection, some instructors also let their students download course lectures. That's up to the instructor though, so make sure you get on their good side!
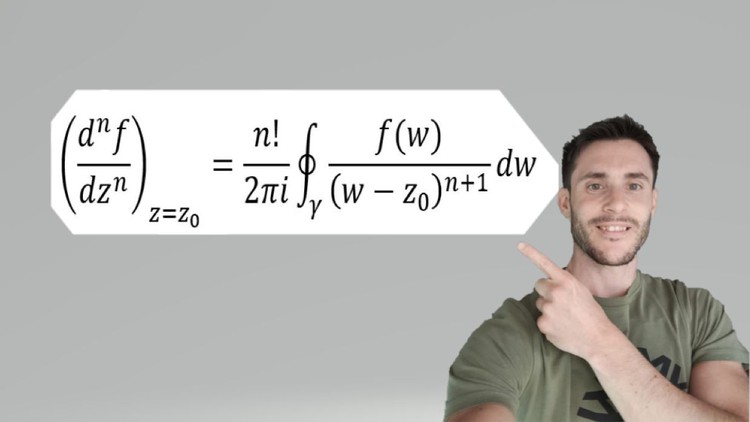
Share
30-Day Money-Back Guarantee
Course details
Video
10 hours
Certificate of Completion
Full lifetime access
Access on mobile and TV
Popular courses
External Links May Contain Affiliate Links read more





