Partial Differential Equations: Comprehensive Course
- Description
- Curriculum
- FAQ
- Reviews
Solving Partial Differential Equations using the Fourier Transform: A Step-by-Step Guide
Course Description:
This course is designed to provide a comprehensive understanding of how the Fourier Transform can be used as a powerful tool to solve Partial Differential Equations (PDE). The course is divided into three parts, each building on the previous one, and includes bonus sections on the mathematical derivation of the Heisenberg Uncertainty Principle.
Part 1: In this part, we will start with the basics of the Fourier series and derive the Fourier Transform and its inverse. We will then apply these concepts to solve PDE’s using the Fourier Transform. Prerequisites for this section are Calculus and Multivariable Calculus, with a focus on topics related to derivatives, integrals, gradient, Laplacian, and spherical coordinates.
Part 2: This section introduces the heat equation and the Laplace equation in Cartesian and polar coordinates. We will solve exercises with different boundary conditions using the Separation of Variables method. This section is self-contained and independent of the first one, but prior knowledge of ODEs is recommended.
Part 3: This section is dedicated to the Diffusion/Heat equation, where we will derive the equation from physics principles and solve it rigorously. Bonus sections are included on the mathematical derivation of the Heisenberg Uncertainty Principle.
Course Benefits:
- Gain a thorough understanding of the Fourier Transform and its application to solving PDE’s.
- Learn how to apply Separation of Variables method to solve exercises with different boundary conditions.
- Gain insight into the Diffusion/Heat equation and how it can be solved.
- Bonus sections on the Heisenberg Uncertainty Principle provide a deeper understanding of the mathematical principles behind quantum mechanics.
Prerequisites:
- Calculus and Multivariable Calculus with a focus on derivatives, integrals, gradient, Laplacian, and spherical coordinates.
- Prior knowledge of ODEs is recommended.
- Some knowledge of Complex Calculus and residues may be useful.
Who is this course for?
- Students and professionals with a background in Mathematics or Physics looking to gain a deeper understanding of solving PDE’s using the Fourier Transform.
- Those interested in the mathematical principles behind quantum mechanics and the Heisenberg Uncertainty Principle.
-
13Setup of the diffusion problemVideo lesson
-
14Integral equation satisfied by the function f(x,t)Video lesson
-
15Diffusion equationVideo lesson
-
16Some possible boundary conditions of the diffusion equationVideo lesson
-
17Solution of the diffusion equation part 1Video lesson
-
18Solution of the diffusion equation part 2Video lesson
-
19Solution of the diffusion equation part 3Video lesson
-
20Solution of the diffusion equation part 4Video lesson
-
26Laplace Equation in Cartesian Coordinates (exercise)Video lesson
-
27Laplace Equation in Polar coordinates (exercise 1)Video lesson
-
28Laplace Equation in Polar coordinates (exercise 2)Video lesson
-
29Laplace Equation in Polar coordinates (exercise 3)Video lesson
-
30Laplace Equation in Polar coordinates (exercise 4)Video lesson
-
31Concept of streamlines (with exercise)Video lesson
-
44How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 1Video lesson
-
45How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 2Video lesson
-
46How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 3Video lesson
-
47How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 4Video lesson
-
48How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 5Video lesson
-
49How Einstein mastered Navier-Stokes equations in hid PhD dissertation Part 6Video lesson
-
53Mathematical summary of how to prove the uncertainty principleVideo lesson
Note: the following lectures will prove the Uncertainty principle more slowly. In this lecture we do it quickly so you can get the idea of how it can be done.
-
54Introduction to the short course on the Heisenberg Uncertainty PrincipleVideo lesson
-
55Probability that a particle exists at a certain timeVideo lesson
-
56Probability that a particle has a certain_energyVideo lesson
-
57Uncertainty in the localization in time and in the energy of the particleVideo lesson
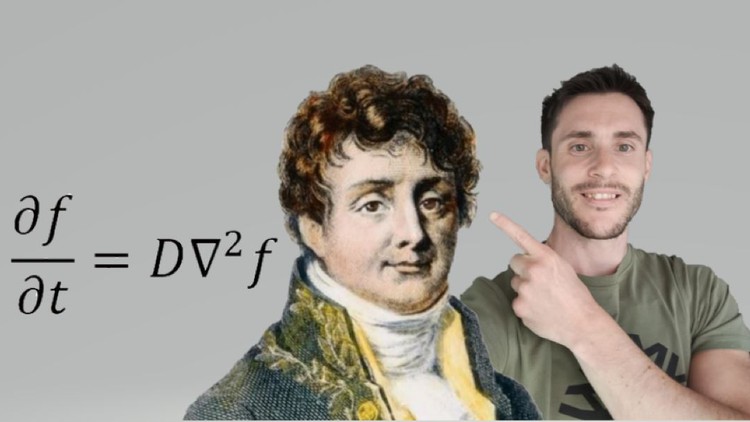
External Links May Contain Affiliate Links read more





