Mathematical intuition behind Special and General Relativity
- Description
- Curriculum
- FAQ
- Reviews
Mastering Special and General Relativity: from the incompatibility between Galileo’s principle and Maxwell’s equations to the unraveling of the greatest “mathematical secrets” of the universe.
Students who take the course will learn the following:
- Understand the incompatibility between Galileo’s principle and Maxwell’s equations.
- Formulate Special Relativity and General Relativity consistently.
- Develop the mathematical intuition required to fully grasp and appreciate the contents of these subjects.
- Learn about Lagrangian mechanics and the Action Principle.
- Understand tensors and their applications in relativity.
- Derive Lorentz transformations in two different ways.
- Learn about the mathematics required to follow the part on General Relativity.
- Meet the prerequisite requirements, including Calculus and Multivariable Calculus.
- Develop skills in problem-solving, critical thinking, and mathematical reasoning.
- Build a strong foundation in advanced physics and mathematics, which can be applied in future studies or research.
Here are some benefits of taking the course on Special and General Relativity:
- Gain a deep understanding of the principles and concepts underlying Special and General Relativity, which are foundational to modern physics and astronomy.
- Develop strong mathematical skills required to fully grasp and appreciate the subject matter, including Lagrangian mechanics and tensor calculus.
- Learn how to derive important equations in Special and General Relativity, including the Lorentz transformations and the Einstein field equations.
- Gain insight into the implications of Special and General Relativity for our understanding of space, time, and gravity, and how these concepts are used in modern physics and astronomy.
- Engage with a challenging and stimulating subject matter, which can help to develop critical thinking skills and problem-solving abilities.
- Potentially open up opportunities for further study or research in the fields of physics, astronomy, or related areas.
- Gain a sense of satisfaction and accomplishment from tackling a complex and challenging subject and mastering its concepts and techniques.
Course description:
- We start by explaining the problem with Galileo’s principle and Maxwell’s equations and how this led to the formulation of Special Relativity.
- We expand the discussion to General Relativity and highlight the importance of mathematical intuition in fully grasping the concepts.
- We motivate every equation in the course to help students understand the underlying principles and theories.
- We provide a comprehensive explanation of Lagrangian mechanics and tensors, which are essential to understanding Special and General Relativity.
- We assume a prerequisite knowledge of Calculus and Multivariable Calculus, including the divergence theorem, vectors, dot and cross products, matrix multiplication, and determinants.
- We suggest some basic knowledge of Classical physics, including scalar potential, Newton’s laws, kinetic energy, energy conservation, and the wave equation.
- The first part of the course will focus on Lorentz transformations and derive them in two different ways, providing a simpler mathematics to follow along.
- The second part of the course will focus on General Relativity, where a pencil and paper are recommended to derive the equations, ensuring that students meet the prerequisite requirements.
- We provide students with a comprehensive understanding of Special and General Relativity and inspire them to appreciate and apply the theories.
- The course is designed for students who are passionate about physics and mathematics, especially those interested in pursuing higher education in these fields.
-
3Lorentz trasformation derivation part 1Video lesson
-
4Lorentz trasformation derivation part 2 - SimultaneityVideo lesson
-
5Lorentz trasformation derivation part 3Video lesson
-
6Lorentz transformation derivation part 4Video lesson
-
7Lorentz transformation derivation part 5Video lesson
-
8Lorentz transformation derivation part 6Video lesson
-
9Lorentz transformation derivation part 7Video lesson
-
10Lorentz invariant quantityVideo lesson
-
11A different derivation of Lorentz transformations part 1Video lesson
-
12A different derivation of Lorentz transformations part 2: rotation matricesVideo lesson
-
13A different derivation of Lorentz transformations part 3Video lesson
-
14A different derivation of Lorentz transformations part 4Video lesson
-
15A different derivation of Lorentz transformations part 5Video lesson
-
16Composition of velocities according to Galileo and LorentzVideo lesson
-
19Introduction to Lagrangian mechanicsVideo lesson
-
20Lagrangian mechanics part 1Video lesson
-
21Lagrangian mechanics part 2Video lesson
-
22Lagrangian mechanics part 3Video lesson
-
23Lagrangian mechanics part 4Video lesson
-
24Additional comments on the Lagrangian, variation of the actionVideo lesson
-
25Derivation of the HamiltonianVideo lesson
-
26Definition of momentumVideo lesson
-
35Tensor transformations part 1Video lesson
-
36Tensor transformations part 2Video lesson
-
37Higher rank tensors from lower rank tensorsVideo lesson
-
38Lower rank tensors from higher rank tensorsVideo lesson
-
39Transformation of Euclidean derivativesVideo lesson
-
40Covariant DerivativeVideo lesson
-
41Some properties of the metric tensorVideo lesson
-
42Christoffel symbol in terms of the metric tensor part 1Video lesson
-
43Christoffel symbol in terms of the metric tensor part 2Video lesson
-
44Covariant derivative of the metric tensorVideo lesson
-
45Covariant derivative of a contravariant vector part 1Video lesson
-
46Covariant derivative of a contravariant vector part 2Video lesson
Note#1: at about 6:41,as I've added in the notes of the last lecture, some tildes are wrong in some expressions, but I will correct them in this lecture.
Note#2: at 15:56 I mention the Ricci tensor: before the Ricci tensor we will introduce the Riemann tensor, but yeah....after that comes the Ricci tensor ;)
-
47Proof that the covariant derivative of the metric tensor is zeroVideo lesson
-
48Equation of a geodesicVideo lesson
-
49Geodesic and parallel transportVideo lesson
-
50Riemann tensor part 1Video lesson
Note: I will do another derivation of the Riemann tensor in the Appendix.
-
51Some properties of : Riemann_tensor, Ricci tensor, Ricci scalarVideo lesson
-
52Action in General RelativityVideo lesson
-
53Invariant 4-volume element in the actionVideo lesson
-
54Determinant of the metric tensorVideo lesson
-
55Variation of the action of gravity part 1Video lesson
-
56Variation of the action of gravity part 2Video lesson
-
57Variation of the action of gravity part 3Video lesson
Note#1: at about 1:04, instead of 'v', there should be 'w'.
Note#2: at about 7:11 'v' should be replaced by 'w'.
-
58Einstein field equations part 1Video lesson
-
59Einstein field equations part 2: another property of the Riemann tensorVideo lesson
-
60Einstein field equations part 3: energy momentum tensorVideo lesson
-
61Field equations in classical physicsVideo lesson
-
62Reducing General Relativity to Newtonian lawsVideo lesson
-
63Final form of the field equationsVideo lesson
-
64Gravitational time dilationVideo lesson
-
65Shell theorem (used in Gravitational time dilation)Video lesson
-
66Lorentz transformations as derived by EinsteinVideo lesson
-
67The physical meaning that Einstein attributed to Lorentz transformationsVideo lesson
-
68How Einstein derived the composition of velocities in SRVideo lesson
-
69How the Maxwell equations in vacuum transform in inertial framesVideo lesson
-
70Relativistic Doppler effect, aberration, transformation of the energyVideo lesson
-
71How Einstein derives his famous equation E=mc^2Video lesson
-
72Dynamics of an accelerated charged bodyVideo lesson
-
73How Einstein shows that the inverse of the metric tensor is also a tensorVideo lesson
-
74How Einstein shows the invariance of the infinitesimal volume elementVideo lesson
-
75How Einstein derives the equation of a geodetic lineVideo lesson
-
76How Einstein derives the concept of covariant derivativeVideo lesson
-
77General Relativity: rule of differentiation of determinantsVideo lesson
-
78How Einstein derives the concept of covariant divergenceVideo lesson
-
79Other important tensor expressions derived by Einstein in his paper on GeneralVideo lesson
-
80How Einstein derives the Riemann tensor in his paper on General RelativityVideo lesson
-
81How Einstein derives the field equations in the absence of matterVideo lesson
-
82How Einstein derives the field equations from the variation principleVideo lesson
-
83How Einstein derives the field equations in the presence of matterVideo lesson
-
84How Einstein derives the energy tensor of a frictionless adiabatic fluidVideo lesson
-
85How Einstein derives Maxwell equations in covariant formVideo lesson
-
86How Einstein shows that his theory of GR reduces to Newtonian physicsVideo lesson
-
87How Einstein calculates the deflection of a light ray due to gravityVideo lesson
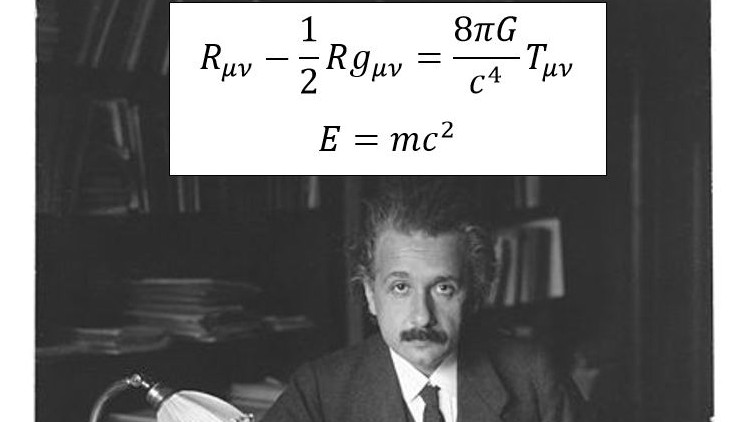
External Links May Contain Affiliate Links read more





